E-Graph Basics

Introduction

An e-graph (equivalence graph) is a type of data structure commonly used to reason about equalities and programs computationally.

Let’s start with a motivating example. Suppose we have a set of relations:

\[ \begin{gather} x = a \\ y = b \\ a = b \\ f(x) = f(y) \end{gather} \]

Given those equations, we might want to ask a few questions: Does \(x = y\)? Does \(f(a) = f(b)\)? If we have many, many equivalences, we will want to be able to quickly answer questions of this nature using a computer.

An e-graph is a way to represent and store “congruence relations”¹: an e-graph compactly represents the relationships among the different terms, and we can use the data structure to check if \(x = y\) and \(f(a) = f(b)\) are valid².

E-graphs are a good data structure for optimizing compilers. Let’s say we have some computation:

z = (x * y) * (x * y)

If we know x and y, we need to do three multiplies to compute z. Instead, we could write the code as follows:

c = x * y
z = c * c

The second example does the same calculation as the first, but with just two multiply operations. Using e-graphs, we can take the following expressions:

z = (x * y) * (x * y)
c = x * y

and conclude

z = c*c

Hopefully, you can see how that might be useful when building an optimizing compiler.

To understand e-graphs better, in this post I implement an e-graph in Python³.

Similar Data Structures

E-graphs draw inspiration from two similar data structures: union-find and hashcons.

Union-Find

A union-find data structure is also used to track equivalence relations among sets of terms. Alternatively, a union-find data set can be thought of as a way to partition a set of terms into disjoint subsets (each disjoint subset is a an equivalence class).

Let’s say we had the following terms: \([a,b,c,d,e,x,y]\). Assume a priori that each term is in its own equivalence class. Then, we introduce some equalities:

\[ \begin{gather} x = a \\ y = b \\ a = b \\ c = d \end{gather} \]

Now, we expect the terms to be distributed into three equivalence classes: \([\{a,b,x,y\},\{c,d\},\{e\}]\).

We should be able to submit a new equality to the union-find data structure and it will automatically handle updating the equivalence classes. Furthermore, since the union-find knows the equivalence classes, if we have some new potential equality (e.g. does \(x = y\)?) we should be able to determine if it is true.

Notice that unlike an e-graph, union-find can’t handle functions with variable arguments: union-find only represents equivalence relations, rather than congruence relations.

Operations

We’re going to assign each equivalence class a “canonical identifier”. For example, if we had \([\{a,b,x,y\},\{c,d\},\{e\}]\), we might choose \([a,c,e]\), respectively.

We’re going to store all of the terms in trees, one tree for each equivalence class. Before introducing any equalities, each term will be in its own tree. The root of each tree will be the canonical identifier for that equivalence class. We’ll merge trees when equalities are introduced that merge equivalence classes.

To do this, we will need two maps:

1. parent (term -> parent term of the input term): Given a term, this map returns another term identifier from the same class (but farther up the tree). In our find method (below) we will recursively repeat this process to find the root node, and hence the identifier for the original term’s equivalence class.

2. rank (term -> rank of that term): Given a term identifier, this map returns some value (usually an integer). In the event two classes need to be merged, the two classes’ ranks determine which canonical identifier of the will be inherited by the new, merged class. A common choice for rank is the size of the equivalence class, but other choices are possible.

If our terms aren’t hashable (for example, if they carry some extra data), we can always keep a third dictionary that maps the identifier for each term to its corresponding data.

Union-find has three major operations:

1. make_set (term -> None): Adds a fresh term to the union-find data structure. This term will be in its own set.

2. find (term -> canonical identifier for that term): Returns the canonical representative of a given equivalence class of terms.

3. union ((equiv_class_id1, equiv_class_id2) -> None): Given two disjoint set ids, combines them into the same set.

Implementation

Let’s implement union-find, to illustrate what is happening.

First, we initialize our maps as dicts in the constructor, as described above.

class UnionFind:

    def __init__(self):
        self.parent = {}
        self.rank = {}

    ...

Next, let’s look at make_set:

class UnionFind:

    ...

    def make_set(self, x):
        if x not in self.parent:
            self.parent[x] = x
            self.rank[x] = 0

    ...

When a new element is added, we assign its rank to \(0\), and we assign it’s parent to itself.

Here’s find:

class UnionFind:

    ...

    def find(self, x):
        if self.parent[x] != x:
            # Path compression
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]

    ...

Let’s consider two cases to analyze what find is doing:

1. Base case: x is it’s own parent. In this case, x is the representative element for it’s own class, so we simply return x.

2. x has a parent. In this case, we do what’s called path compression. First, we find the representative element for x’s parent. Then, we set x’s parent to that representative element. Note that if x’s parent also has a parent, which also has a parent, etc., find runs the same steps recursively on x’s parent, on and on up the tree. In essence, what this does is “flatten” the tree above x. Now x and all of x’s ancestors point directly to the canonical class identifier. Once this is all done, we return the highest ancestor, which is the canonical identifier for that class.

Here’s an illustration of path compression. In the illustration, path compression starts from node 7. All of node 7’s ancestor end up pointing to the root.

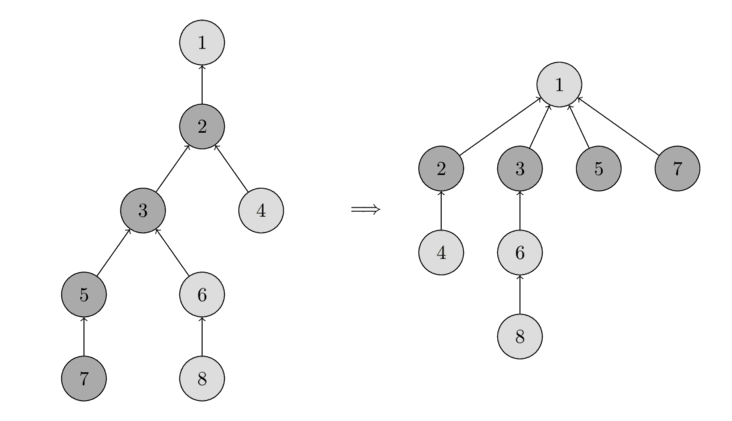
The last operation is union:

class UnionFind:

    ...
    
    def union(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)

        if root_x != root_y:
            if self.rank[root_x] < self.rank[root_y]:
                self.parent[root_x] = root_y
            elif self.rank[root_x] > self.rank[root_y]:
                self.parent[root_y] = root_x
            else:
                self.parent[root_y] = root_x
                self.rank[root_x] += 1
    ...

If the two canonical identifiers for x and y are the same, the classes are already merged, and we do nothing.

If the classes aren’t the same, we check the ranks of x and y. If they have different ranks, we make the canonical element of the lower ranked element the parent of the higher ranked representative. And that’s it, the classes are combined: any find on an element of the higher ranked class will now return the canonical representative of the lower ranked class!

If the ranks are the same, we need some way to decide which of the two representatives will be the new representative. In this implementation, it’s arbitrary (decided by the order of the arguments x and y). However, in practice you may want to use different methods to make this decision: it could be the size of the equivalence classes (larger set wins?), the “simpler” representative wins (whatever that might mean), or some other method.

And that’s it! Let’s test our union-find implementation:

def test_unionfind():
    uf = UnionFind()

    # Adding elements
    for char in "abcdexy":
        uf.make_set(char)

    # Performing unions
    uf.union("x", "a")
    uf.union("y", "b")
    uf.union("a", "b")
    uf.union("c", "d")

    # Test 
    assert "x" == uf.find("a") 
    assert "x" == uf.find("b")
    assert "e" == uf.find("e")
    assert uf.find("x") == uf.find("y") # checks x ?= y

Hashcons

Hashcons is a simple technique to determine if two objects are equivalent in constant time. We maintain a hash table, where each hash points to an associated list of objects. When we construct a new element, we hash it, then check to see if that hash already exists in the hashtable.

If the element doesn’t exist in the hash table, it’s a unique element, and we add it to our hash table and construct a list. If the element does exist, we place the object in the associated list for that hash id and return the existing object in that list.

As a result of this, two object instances that differ in memory will still be equivalent, so long as they hash to the same value.

Let’s demonstrate in Python:

class HashCons:
    def __init__(self):
        self.store = {}

    def cons(self, obj):
        hash_id = hash(obj)
        if hash_id in self.store.keys():
            return self.store[hash_id]
        else:
            self.store[hash_id] = obj
            return obj

def test_hashcons():
    hs = HashCons()

    tuple1 = ("x", "+", "y")
    tuple2 = ("x", "+", "y")

    # Different objects
    assert tuple1 is not tuple2 

    hashed_tuple1 = hs.cons(tuple1)
    hashed_tuple2 = hs.cons(tuple2)

    # But same values
    assert hashed_tuple1 is hashed_tuple2 

Note that if we were to check tuple1 == tuple2 in Python, without consing the tuples, Python would return True. That’s because in Python, is compares the memory addresses of objects, whereas == compares their values.

E-Graph

Now that we understand both union-find and hashcons, we can implement e-graphs.

Preliminaries

We’re going to need two helper classes: one for storing e-nodes, one for storing e-classes.

An e-class is what you’d expect: a set of e-nodes. An e-node is a representation of a term or operator over terms. For the sake of this discussion, let’s use what I’ll call arithmetical terms as the unit of interest. To represent an arithmetical term in Python, we will use a tuple: the first element of the tuple will be an arithmetical operation (i.e. plus, minus, multiply, etc.). The second element of the tuple will be the set of arguments for that operation. For example, we might have:

# Unitary terms are just symbols, with no arguments. 
# This represents the integers 1,2,3.
one = ('1', ())
two = ('2', ())
three = ('3', ())

# Here's some "computations":. 
term4 = ('+', (one, two))
term5 = ('+', (two, one))
term6 = ('*', (three, one))

It might seem odd to represent integers as objects⁴, but we need to represent programs in Python if we are going to manipulate programs using Python⁵.

Now, let’s define classes to wrap these gadgets up:

class ENode:

    def __init__(self, op, args):
        self.op = op 
        self.args = args 

    def __eq__(self, other):
        ops_equal = self.op == other.op 
        args_equal = self.args == other.args
        return ops_equal and args_equal

    def __hash__(self):
        return hash((self.op, self.args))

    def __repr__(self):
        return f"ENode({self.op}, {self.args})"

Above is our e-node implementation. The dunder method __hash__ in Python is used to make the class hashable. You may start to see a resemblance to hashcons.

class EClass:
    def __init__(self, id_):
        self.id = id_
        self.nodes = set()

    def __repr__(self):
        return f"EClass({self.id}, {self.nodes})"    

As mentioned, the e-class just holds a set of e-nodes.

Operations

Now let’s discuss what goes into an e-graph.

We need to maintain a few maps, similar to union-find:

1. classes (eclass_id -> eclass): Given an e-class id, this map will return the relevant EClass object.

2. parents (eclass_id -> enode_id): this is similar to union-find. However, unlike in union-find, given an e-class id, this returns the id for the e-node that points to that e-class. The e-node might be representing a larger e-class, or it might not. This is key to understanding the e-graph: an e-node has e-classes as it’s arguments rather than other e-nodes and an e-class has e-nodes as it’s parents.

3. enode_to_eclass (enode -> eclass_id): similar to hashcons, given the hash value of an e-node, this returns the id of the eclass that contains it.

In terms of methods:

1. add (enode -> None): analogous to make_set in union-find. Either the e-node is already in an e-class, or we merge it in. For “constant nodes” (i.e. for arithmetical terms, these are nodes without arguments, which might be symbols like “1”, “2”, etc.), we create a new e-class and set it as it’s own id. However, for nodes with arguments, we have one additional step, which is to identify any congruent nodes and merge them into a single e-class. This is discussed in more detail below.

2. find (term -> canonical id for that term): this is basically exactly the same find as in union-find. Given the id for an e-class, get the canonical representative for that e-class, and compress the path along the way.

3. union ((term_id1, term_id2) -> merged term id): this is also very similar to the union in union-find. Given two e-class ids, we find their canonical representatives, then merge them into a single class by setting the root of one class and the parent to the other root. Unlike in union-find, we will also need to do some bookkeeping around the classes and enode_to_eclass mappings

4. rebuild (()-> None): When we add to an e-graph, or modify it with union, the congruence relations may become stale. Rebuild checks to see if the canonical representations for any arguments of any e-nodes have changed, and if so, updates them across the board. This operation is usually a linear scan across the e-graph, so we have to make a choice: we can automatically call this function after every add or union (ensuring queries never return stale results) or we can let the user choose when to call the method (amortizing the cost of running the method).

5. extract (id -> None): We will add a nifty helper method to print out the canonical form of a node. Strictly speaking, this isn’t necessary.

Implementation

Let’s take a look at the actual code for an e-graph.

First, we build out the constructor:

class EGraph:

    def __init__(self):
        self.classes = {}
        self.parents = {}
        self.enode_to_id = {}
        self.next_id = 0

    ...

Simple enough. The add function:

class EGraph:
    
    ...

    def _get_next_eclass_id(self):
        id_ = self.next_id
        self.next_id += 1
        return id_

    def add(self, enode):
        if enode in self.enode_to_eclass_id:
            return self.find(self.enode_to_eclass_id[enode])
    
        # Allocate a new id
        eclass_id = self._get_next_eclass_id()

        # Create a new eclass 
        self.classes[eclass_id] = EClass(eclass_id)
        self.classes[eclass_id].nodes.add(enode)
        self.enode_to_eclass_id[enode] = eclass_id
        self.parents[eclass_id] = eclass_id 
    
        # Skip merging for constant nodes
        if not enode.args:
            return eclass_id
        
        # Only union with congruent nodes
        for other_node in list(self.enode_to_eclass_id.keys()):
            ops_equal = other_node.op == enode.op
            args_equal_len = len(other_node.args) == len(enode.args)
            
            if ops_equal and args_equal_len:

                for arg1, arg2 in zip(other_node.args, enode.args):
                    arg1_canonical = self.find(arg1)
                    arg2_canonical = self.find(arg2)
                    if arg1_canonical != arg2_canonical:
                        break # If any arguments don't match, stop

                else: # Runs only if all arguments match
                    other_class = self.enode_to_eclass_id[other_node]
                    other_canonical_id = self.find(other_class)
                    union = self.union(eclass_id, other_canonical_id)
                    return union
            
        return eclass_id
 
    ...

The first part is similar to hashcons: we check if the enode already exists, and if it does, we return it’s canonical identity and return it. If it doesn’t exist, the next part is make_set, but we also have to run a linear scan of all of the other enodes and union them if they are identical to the new enode (in terms of canonical representations).

class EGraph:

    ...

    def find(self, id_):
        if id_ not in self.parents:  
            self.parents[id_] = id_
        if self.parents[id_] != id_:
            self.parents[id_] = self.find(self.parents[id_])
        return self.parents[id_]
    
    ...

find is basically the same as in union-find. Not much more to say.

class EGraph:

    ...

    # union by size of e-class 
    def _compare_eclass_rank(self, rep1, rep2):
        rank1 = len(self.classes[rep1].nodes)
        rank2 = len(self.classes[rep2].nodes)
        if rank2 > rank1:
            return rep2, rep1
        else: 
            # root1 wins ties
            return rep1, rep2 

    def union(self, id1, id2):
        rep1, rep2 = self.find(id1), self.find(id2)

        if rep1 == rep2:
            # No need to merge if they're the same eclass
            return rep1
        
        ranked_reps = self._compare_eclass_rank(rep1, rep2)
        parent_rep, child_rep = ranked_reps

        # Update the child rep's parents
        self.parents[child_rep] = parent_rep

        # For each node in the child rep, update its parents
        child_nodes = self.classes[child_rep].nodes
        self.classes[parent_rep].nodes.update(child_nodes)
        for node in self.classes[child_rep].nodes:
            self.enode_to_eclass_id[node] = parent_rep

        # Delete the child eclass, since it's now merged
        del self.classes[child_rep]

        return parent_rep
    
    ...

Union is also very similar to union find. We have a helper method here for deciding which canonical element takes precedence. In this implementation, the class with more nodes wins out, but you could override this method with some other criteria.

class EGraph:

    ...

    def rebuild(self):

        # Maintain a queue of nodes to be processed
        pending_nodes = list(self.enode_to_eclass_id.items())
    
        while pending_nodes:
            enode, initial_id = pending_nodes.pop(0)
            current_id = self.find(initial_id)
            new_args = tuple(self.find(arg) for arg in enode.args)
        
            if new_args != enode.args:
                new_enode = ENode(enode.op, new_args)

                # Remove the old enode
                self.classes[current_id].nodes.remove(enode)
                del self.enode_to_eclass_id[enode]

                # Add the new enode
                new_id = self.add(new_enode)

                # Merge  
                if self.find(current_id) != self.find(new_id):
                    self.union(current_id, new_id)

                # This is a fixpoint operation
                # We will need to check the new node again
                # Add it to the end of the queue
                pending_nodes.append((new_enode, new_id))
    ...

The major new operation is rebuild. Nodes have arguments, so we need to check to see if the canonical identifiers have changed. We keep going until the e-graph converges.

class EGraph:

    ...

    def _rank_enodes(self, enode):
        # rank by size, then by lexical order
        # smallest number of args wins, then first alphabetically
        return (len(enode.args), enode.op)

    def extract(self, id_) :
        root = self.find(id_)
        eclass = self.classes[root]
        best_node = min(eclass.nodes, key=self._rank_enodes)
        if not best_node.args:
            return best_node.op
        canon_args = [self.extract(arg) for arg in best_node.args]
        return (best_node.op,) + tuple(canon_args)

    ...

As described, extract is just a helper function to print out the type. We also have a helper method for choosing which node is the best representation. Here, we are choosing based on fewest arguments⁶.

In the next section we will look at some use cases.

Use Cases

Let’s look at some toy examples.

Basic Arithmetic

In the first test, we check if \(1 + 2 = 2 + 1\).

def test_egraph_arithmetic():
    egraph = EGraph()

    # Add some expressions
    var = lambda name: egraph.add(ENode(name, ()))
    const = lambda x: egraph.add(ENode(str(x), ()))
    plus = lambda x, y: egraph.add(ENode('+', (x, y)))

    var_x, var_y = var('x'), var('y')
    one, two, three = const(1), const(2), const(3)
    expr1 = plus(one, two)  # 1 + 2
    expr2 = plus(two, one)  # 2 + 1 - note that this is never unioned 

    egraph.union(var_x, one) # Set x = 1
    egraph.union(var_y, two) # Set y = 2
    egraph.union(expr1, three) # 1 + 2 == 3
    egraph.union(plus(var_x, var_y), plus(var_y, var_x))

    # Rebuild to propagate changes
    egraph.rebuild()

    # Since we know x + y == y + x, we can conclude 1 + 2 == 2 + 1
    assert egraph.extract(expr1) == egraph.extract(expr2)

    # Since we know 1 + 2 == 3, and we know commutativity, 2 + 1 == 3
    assert egraph.extract(expr2) == egraph.extract(three) 

Code Optimization

In the second test, we return to our optimizing compiler example from earlier:

def test_egraph_multiplication_optimization():
    egraph = EGraph()

    mul = lambda a, b: egraph.add(ENode('*', (a, b)))
    var = lambda name: egraph.add(ENode(name, ()))
    
    x = var('x')
    y = var('y')    
    
    c = var('c')
    expr1 = mul(x, y)
    egraph.union(c, expr1) 
    
    expr2 = mul(mul(x, y), mul(x, y))

    egraph.rebuild()

    print(egraph.extract(expr2)) # prints (*, 'c', 'c')
    assert egraph.extract(expr2) == egraph.extract(mul(c, c))

    return egraph

Other Considerations

The naive e-graph implementation we have here may have a few issues for serious use cases:

Runtime

find and union are both constant-time operations, but in the worst-case scenario add and rebuild need to run linear scans over all of the arguments for all of nodes in the e-graph. These are \(O(n*k)\) operations, if n is the number of nodes and k is the maximum number of arguments. This is especially expensive if we are rebuilding frequently.

Memory

The size of the data structure is linear in the number of classes and nodes, but even a small number of terms can lead to a huge number of equivalent expressions. For example, if we are summing \(n\) variables, there are many ways to place parentheses among the terms without changing the sum⁷.

Cycles

E-graphs can represent potentially infinitely nested expressions by using cycles. Suppose we have \(f(x)=1*x\). Then \(f(f(x))=f(x)\), \(f(f(f(x))) = f(f(x))\), etc.

Here’s a quick example of this in action, using our e-graph implementation:

def test_loop_equivalence():
    egraph = EGraph()

    var = lambda name: egraph.add(ENode(name, ()))
    const = lambda x: egraph.add(ENode(str(x), ()))

    x = var('x')
    one = const('1')

    mult1 = lambda y: egraph.add(ENode('*', (one, y)))
    mult1x = mult1(x)
    mult11x = mult1(mult1x)
    mult111x = mult1(mult11x)
    mult1111x = mult1(mult111x)
    
    # Set 1*x = x 
    egraph.union(mult1x, x)
    
    egraph.rebuild()

    # These should all be equivalent
    assert egraph.find(mult1x) == egraph.find(x)
    assert egraph.find(mult11x) == egraph.find(mult111x)
    assert egraph.find(mult1111x) == egraph.find(mult111x)

    print(egraph.extract(mult1111x)) # Prints x

    return egraph

What’s happening? The e-node (*, 1, 'x') contains x. But when we unify x with (*, 1, 'x'), they end up in the same e-class!

Summary

I implemented a simple e-graph and looked at some toy examples. The code is available on Github.

In future posts, I will attempt to use these data structures for automated reasoning.

Learn More

Check out the following sources to learn more about e-graphs:

1. Check out this paper or this paper, I believe these are the origination of the data structure (although they do not use the term e-graph).

2. Phillip Zucker has many interesting posts about e-graphs.

3. Talia Ringer’s course notes on dependent types has information about e-graphs.

4. There’s a package called egg (written in Rust) that implements e-graphs. There are also Python bindings for egg.

5. This blog post by Cole K is also excellent, especially if you learn by illustrations.

Footnotes

1. “Equality” means different things in different contexts. This post will mostly gloss over the differences, although eventually I will write a post on this subject. An “equivalence relation” on a set of terms is a binary relation that is reflexive (\(a=a\)), symmetric (\(a=b\) \(\Rightarrow\) \(b=a\)), and transitive (\(a=b\) and \(b=c\) \(\Rightarrow\) \(a=c\)). A relation is a “congruence relation” if it is an equivalence relation, and any n-ary operation on equivalent terms returns equivalence terms (that is, if \(a_1=b_1\), \(a_2=b_2\), etc., then \(f(a_1,a_2,...,a_n)=f(b_1,b_2,...,b_n)\)). For a deeper dive into equality, see this talk by Kevin Buzzard. For now, Euclid’s first common notion will suffice.

2. An important subtlety here is that these congruence relations are purely syntactic: the e-graph will not evaluate \(f(a)\) to see what it returns: it will just unify the relevant variables and compare the symbols.

3. Python is probably not a good choice for this task, in general. However, I’ve chosen Python because (a) I didn’t see any Python examples on the web with a cursory search (b) most people know some Python and (c) I eventually want to do some machine-learning-related tasks with these data structures, and having a Python-native implementation will come in handy.

4. Python itself actually implements (small) integers as objects.

5. We could manipulate Python’s abstract syntax tree directly (with the ast module), but it’s out of scope for this post.

6. Extraction is actually NP-Complete in general.

7. This is described by the Catalan numbers.