Differentiable Game Canonicalization

Introduction

Given two games, how can we tell if they are “strategically equivalent”?

For example, consider the following 2x2 games:

Game A: \[ \begin{array}{c|cc} & L & R \\ \hline U & (3,3) & (0,5) \\ D & (5,0) & (1,1) \end{array} \]

Game B: \[ \begin{array}{c|cc} & X & Y \\ \hline A & (10,10) & (25,4) \\ B & (4,25) & (16,16) \end{array} \]

They have different players, action labels, and payoff values. But strategically, both are “equivalent” (to Battle of the Sexes).

In this post, we build a game “canonicalizer” for 2x2 strict ordinal games. This allows a user to quickly identify the game type based on the payoff matrix¹. Furthermore, this implementation is end-to-end differentiable, so it can be plugged into a PyTorch deep learning pipeline.

Example use cases might be fast lookup in a “game zoo” database, curriculum learning for agents (train on progressively “harder” games), boundary analysis², or graph search over ordinal neighborhoods.

What’s in a Game?

We consider a game to be “finite normal form” if the following conditions are all true:

1. There is a finite set of \(n\) players, indexed by \(i\).
2. Each player has \(k\) possible finite pure strategies they can play, denoted \(S_i = {1,2,...k}\).
3. There is a payoff function \(u_i\) for each player such that

\[ u_i: S_1 \times S_2 \times ... \times S_{n} \to \mathbb{R} \]

We can stack these to form a tensor:

\[ U \in \mathbb{R}^{P \times S_1 \times ... \times S_{P}} \]

For a 2-player, 2-strategy game, this is simply two 2x2 matrices, or one 2x2x2 tensor³.

We say a game is a “strict ordinal” game if all the payoffs for each player are distinct. For 2×2 games, each player has exactly 4 outcomes, ranked 1st through 4th (or 0-3 in my implementation).

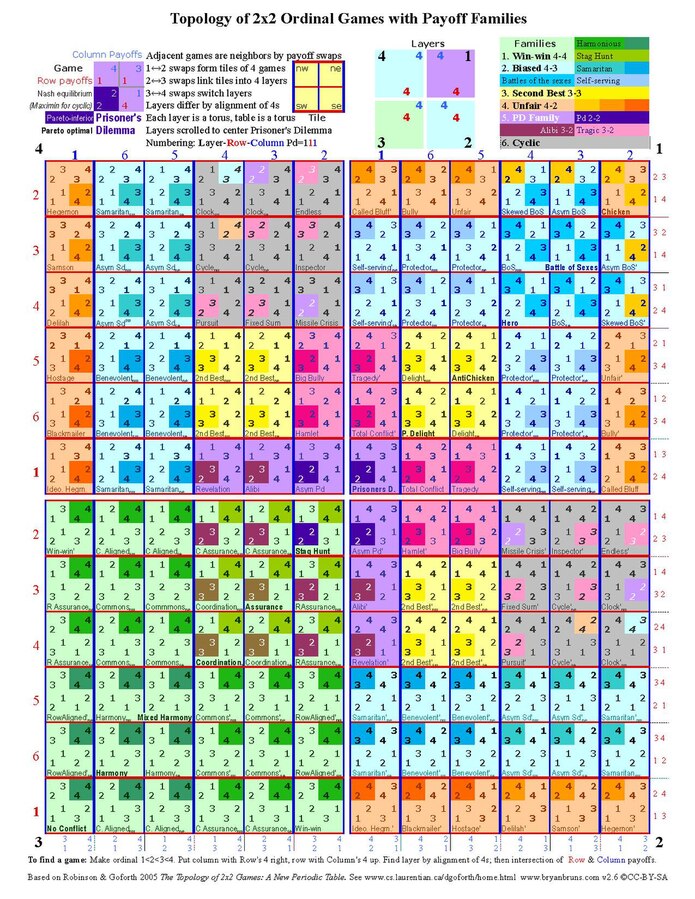
There are \(4! \times 4! = 576\) possible strict ordinal 2x2 games, but many are “strategically equivalent”. In their 2005 book, Robinson and Goforth note that accounting for “strategic equivalence” leaves us with 144 strict ordinal 2x2 games. They go on to arrange these in a periodic table⁴:

The periodic table organizes the 144 canonical strict ordinal 2x2 games into a structured topology. Each cell represents a unique game type, with well-known games highlighted in colored regions. Moving horizontally changes one player’s preference ordering, while vertical movement affects the other player’s. Adjacent games differ by a single ordinal swap, creating natural “neighborhoods” in game space.

Strategic Equivalence

Two games are “strategically equivalent” if “rational” players would behave identically in both games. There are different ways to formalize this notion. Commonly, we require that the games have the same Nash equilibria⁵.

Nash Equilibria

A Nash equilibrium is a situation where no player could gain more by changing their own strategy (holding all other players’ strategies fixed).

Formally, a strategy profile \(s^* = (s_1^*, ..., s_n^*)\) is a Nash equilibrium if for all players \(i\) and all alternative strategies \(s_i \in S_i\):

\[ u_i(s_i^*, s_{-i}^*) \geq u_i(s_i, s_{-i}^*) \]

where \(s_{-i}\) denotes the strategies of all players except \(i\).

In other words, each player’s strategy is a best response to the other players’ strategies. For 2x2 games, this can be computed by checking each cell to see if either player wants to deviate unilaterally.

Equilibria-Preserving Transformations

It’s well-known⁶ that Nash equilibria are preserved under the following three actions:

1. per‑player positive affine transforms.
2. permuting actions per player.
3. permuting player order.

Positive Affine Transformations

For each player \(i\), let \[ u'_i(s)\;=\;a_i\,u_i(s)+b_i,\qquad a_i>0,\; b_i\in\mathbb{R}. \]

Claim. Best responses and Nash equilibria are unchanged by \(u_i\mapsto u'_i\).

Proof. For fixed each player \(i\), \(s_{-i}\), \[ \begin{align} \arg\max_{s_i} u'_i(s_i,s_{-i}) &= \arg\max_{s_i}\big(a_i\,u_i(s_i,s_{-i})+b_i\big)\\ &= \arg\max_{s_i} u_i(s_i,s_{-i}) \end{align} \] because \(z\mapsto a_i z+b_i\) is strictly increasing. Thus, the Nash set is invariant.\(\square\)

Action Permutations

Let \(\pi_i:S_i\to S_i\) be a permutation for each player \(i\). Define the relabeled game by \[ u_i^\pi(s_1,\ldots,s_n)=u_i\!\big(\pi_1^{-1}(s_1),\ldots,\pi_n^{-1}(s_n)\big). \]

Claim. Nash equilibria are preserved under action relabeling.

Proof. Consider a strategy profile \(s^* = (s_1^*, \ldots, s_n^*)\) that is a Nash equilibrium in the original game. We show that \(s^\pi = (\pi_1(s_1^*), \ldots, \pi_n(s_n^*))\) is a Nash equilibrium in the relabeled game.

In the original game, for each player \(i\) and any alternative strategy \(s_i\): \[u_i(s_i^*, s_{-i}^*) \geq u_i(s_i, s_{-i}^*)\]

In the relabeled game, for any deviation to action \(t_i \in S_i\): \[ \begin{align} u_i^\pi(t_i, \pi_{-i}(s_{-i}^*)) &= u_i(\pi_i^{-1}(t_i), s_{-i}^*) \\ &\leq u_i(s_i^*, s_{-i}^*) \\ &= u_i^\pi(\pi_i(s_i^*), \pi_{-i}(s_{-i}^*)) \end{align} \]

Thus no player can improve by deviating in the relabeled game.

The mapping \(s \mapsto (\pi_1(s_1), \ldots, \pi_n(s_n))\) is a bijection between strategy profiles, establishing a one-to-one correspondence between Nash equilibria in the original and relabeled games.

Player Permutations

Let \(\sigma\) be a permutation of players. Define \(G^\sigma\) by reindexing: \[ S'_i:=S_{\sigma^{-1}(i)},\qquad u'_i(s'):=u_{\sigma^{-1}(i)}\!\big(T_{\sigma^{-1}}(s')\big), \] where \(T_{\sigma^{-1}}\) reorders the profile \(s'\) back to the original coordinate order.

Claim. Permuting player order preserves Nash equilibria.

Proof. Similar to action permutations. Consider a strategy profile \(s^* = (s_1^*, \ldots, s_n^*)\) that is a Nash equilibrium in the original game. We show that \(s'\) defined by \(s'_i = s^*_{\sigma^{-1}(i)}\) is a Nash equilibrium in \(G^\sigma\).

In the original game, for each player \(j\) and any alternative strategy \(s_j\): \[u_j(s_j^*, s_{-j}^*) \geq u_j(s_j, s_{-j}^*)\]

In the reindexed game \(G^\sigma\), for player \(i\) considering deviation to strategy \(t_i \in S'_i\): \[ \begin{align} u'_i(t_i, s'_{-i}) &= u_{\sigma^{-1}(i)}(T_{\sigma^{-1}}(t_i, s'_{-i})) \\ &= u_{\sigma^{-1}(i)}(t_i, s^*_{-\sigma^{-1}(i)}) \\ &\leq u_{\sigma^{-1}(i)}(s^*_{\sigma^{-1}(i)}, s^*_{-\sigma^{-1}(i)}) \\ &= u'_i(s'_i, s'_{-i}) \end{align} \]

Thus no player can improve by deviating in the reindexed game.

The mapping \(s \mapsto s'\) where \(s'_i = s_{\sigma^{-1}(i)}\) is a bijection between strategy profiles, establishing a one-to-one correspondence between Nash equilibria in the original and reindexed games. \(\square\)

Example

Returning to our original example, we can transform Game A into Game B via:

1. Affine transformation: Transform both players payoffs by \(f(x) \to 3x + 7\).
2. Relabel actions: \(U \to D\) for Player 1, \(L \to R\) for Player 2
3. Relabel players: Swap Player 1 and Player 2

Thus, Game A and Game B are in some sense “equivalent”. We can also think about decomposing the original game into a tuple consisting of the canonical id, permutations on the row and columns, and an affine transformation, wherein Game A and Game B are equal in the first entry.

Differentiable Permutations

Our goal is to construct an invariant, differentiable, and deterministic function that maps a given game to it’s canonical representation. To do this, we will need to implement differentiable versions of each type of transformation that preserves the Nash equilibria. Since positive affine transformations are already differentiable, we just need a way to differentiably handle permutations. For this post we solve the differentiability problem by using the Sinkhorn algorithm to generate “soft” permutations⁷.

Doubly-Stochastic Matrices

Permutation matrices are discrete, but we can approximate them with doubly-stochastic matrices (non-negative matrices where rows and columns sum to 1).

A permutation matrix \(P\) has exactly one 1 in each row and column, with all other entries being 0. For example, the permutation that swaps two items: \[ P = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \]

A doubly-stochastic matrix relaxes this constraint: entries can be any values in \([0,1]\), as long as each row sums to 1 and each column sums to 1. For example: \[ P_\text{soft} = \begin{bmatrix} 0.2 & 0.8 \\ 0.8 & 0.2 \end{bmatrix} \]

This “soft” permutation mostly swaps the items (0.8 weight) but keeps some probability mass (0.2) on not swapping. As we make the entries more extreme (closer to 0 or 1), we approach a hard permutation.

Sinkhorn Algorithm

The Sinkhorn algorithm iteratively normalizes a matrix to make it doubly-stochastic. We start with a matrix \(M\) containing positive entries \(s\).

We first create a cost matrix

\[ C_{ij} = (s_i - p_j)^2 \] where \(p_j\) are target positions.

Then, we convert to “soft positions” \(M_{ij} = \exp(-C_{ij}/\tau)\) with temperature \(\tau > 0\).

Finally, we alternate normalizing the rows and columns until converged (usually 20-30 iterations).

Practical Considerations

The algorithm is guaranteed to converge to a unique solution for strictly positive matrices.

Since we use \(M = \exp(-C/\tau)\), all entries are positive. In practice, we work in log-space for numerical stability. As temperature \(\tau \to 0\), the soft permutation approaches a hard permutation while remaining differentiable.

When scores are identical, the cost matrix has ties and the soft permutation becomes ambiguous. We break ties using secondary criteria:

\[ s_i^{\text{final}} = s_i^{\text{mean}} + \epsilon_1 \cdot s_i^{\text{var}} + \epsilon_2 \cdot s_i^{\text{max}} \]

where \(s_i^{\text{mean}}\) is the mean score, \(s_i^{\text{var}}\) is the variance, \(s_i^{\text{max}}\) is the maximum, and \(\epsilon_1, \epsilon_2 \ll 1\) are tiny weights. This ensures a deterministic ordering even for symmetric games.

Finally, we need to handle permutations on multiple axes. To manage this, we compute all permutations from the original ordinal rankings, then apply them in a fixed order. This ensures the canonicalization is consistent and differentiable end-to-end.

Implementation

Now that we have differentiable permutations, here is our general approach for implementing the key functions:

1. Convert payoffs to ordinal rankings.
2. Apply soft permutations to sort players and actions.
3. Use temperature annealing to sharpen soft permutations.
4. Generate a unique hash to identify the game.

We’ll organize this code as a GameCanonicalizer class. The remaining functions will be methods.

import torchsort
import torch 
from torch import nn

import hashlib
from scipy.optimize import linear_sum_assignment as hungarian

class GameCanonicalizer(nn.Module):
    
    def __init__(
            self, 
            num_players: int, 
            tau_players: float = 0.02, 
            tau_actions: float = 0.02, 
            sinkhorn_iters: int = 30,
            rank_reg: float = 1e-4, 
            tiny_tie: Tuple[float, float] = (1e-3, 1e-6)
            ):
        super().__init__()

        self.num_players = num_players

        self.rank_reg = rank_reg
        self.tau_players = tau_players
        self.tau_actions = tau_actions
        self.sinkhorn_iters = sinkhorn_iters
        self.tiny_tie = tiny_tie

Ordination

First, we create our ordinal values using torchsort’s soft_rank function, which uses projections onto the permutahedron to generate differentiable ranks.

    def ordinate(self, payoffs: torch.Tensor) -> torch.Tensor:
        original_shape = payoffs.shape
        flattened = payoffs.reshape(self.num_players, -1) 
        rankings = torchsort.soft_rank(flattened, regularization_strength=self.rank_reg)
        return rankings.view(original_shape)

Soft Permutations

Next, we need to implement our soft permutations.

Sinkhorn

We’ll start with the Sinkhorn algorithm itself:

   def sinkhorn(self, log_alpha: torch.Tensor, n_iters: int = 30, eps: float = 1e-9) -> torch.Tensor:
        log_P = log_alpha
        for _ in range(n_iters):
            log_P = log_P - torch.logsumexp(log_P, dim=1, keepdim=True) # rownorm
            log_P = log_P - torch.logsumexp(log_P, dim=0, keepdim=True) # colnorm
        return torch.exp(log_P).clamp_min(eps)

We convert to log-space, then alternate normalizing the rows and columns, as described above. Finally, we exponentiate again.

Converting Scores to Permutations

Now that we have the Sinkhorn method, we need to run it. The soft_perm_from_scores method creates these soft permutations from scores by first normalizing scores to \([0,1]\), then computing a quadratic cost matrix between scores and target positions, then applying Sinkhorn.

    def soft_perm_from_scores(self, scores: torch.Tensor, tau: float = 0.05, n_iters: int = 30) -> torch.Tensor:
        n = scores.shape[0]
        positions = torch.linspace(0.0, 1.0, n, device=scores.device, dtype=scores.dtype)
        s = (scores - scores.min()) / (scores.max() - scores.min() + 1e-12) 
        cost = (s[:, None] - positions[None, :]) ** 2  
        log_alpha = -cost / (2 * tau)  
        P = self.sinkhorn(log_alpha, n_iters=n_iters) 
        return P  

Scoring Functions with Tie-Breaking

Where do we get the scores from in the previous section? The _action_scores and _player_scores methods compute summary statistics for each action or player from the ordinal tensor. Both use the mean as the primary score, with variance and maximum as tie-breakers weighted by tiny constants. This ensures a deterministic ordering even for symmetric games where multiple permutations could be valid.

    def _action_scores(self, ordinal: torch.Tensor, player_idx: int) -> torch.Tensor:
        axes = list(range(ordinal.ndim))
        reduce_axes = [a for a in axes if a != player_idx]
        mean = ordinal.mean(dim=reduce_axes)
        var = ordinal.var(dim=reduce_axes, unbiased=False)
        mx = ordinal.amax(dim=reduce_axes)
        w_var, w_max = self.tiny_tie
        return mean + w_var * var + w_max * mx  

    def _player_scores(self, ordinal: torch.Tensor) -> torch.Tensor:
        P = ordinal.shape[0]
        flat = ordinal.reshape(P, -1)   
        mean = flat.mean(dim=1)
        var  = flat.var(dim=1, unbiased=False)
        mx   = flat.max(dim=1).values
        w_var, w_max = self.tiny_tie
        return mean + w_var * var + w_max * mx 

Applying Permutations to Tensors

We also need to be able to apply permutations to tensors. The _mode_matmul method applies a permutation matrix to a specific axis of a tensor. Since matrix multiplication only works on 2D tensors, we permute dimensions to bring the target axis to the front, apply the permutation matrix transpose (which maps items to their sorted positions), then permute back. This allows us to sort along any axis of our multi-dimensional payoff tensor.

    @staticmethod
    def _mode_matmul(t: torch.Tensor, P: torch.Tensor, axis: int) -> torch.Tensor:

        perm = list(range(t.ndim))
        perm[axis], perm[0] = perm[0], perm[axis]
        t_perm = t.permute(perm) 
        n = t_perm.shape[0]
        assert P.shape == (n, n)
        
        t_sorted = torch.tensordot(P.T, t_perm, dims=([1], [0]))  
        inv = list(range(t.ndim))
        inv[0], inv[axis] = inv[axis], inv[0]
        return t_sorted.permute(inv)

Forward Pass

Now that we have the above methods, we can put them together. The forward method orchestrates the soft canonicalization process. First, it converts payoffs to ordinal rankings. Then it computes action permutations for each player from the original ordinals and applies them to their respective axes (axes 1, 2, etc.). Finally, it computes and applies the player permutation on axis 0. The key insight is that action permutations are computed from the original ordinals before any transformations, ensuring consistency—each player’s actions are sorted based on their own payoffs, not influenced by other permutations.

def forward(self, payoffs: torch.Tensor) -> torch.Tensor:
        P = payoffs.shape[0]
        ordinated_payoffs = self.ordinate(payoffs)

        P_actions = []
        for i in range(P):
            s_actions = self._action_scores(ordinated_payoffs[i], player_idx=i)
            P_i = self.soft_perm_from_scores(s_actions, tau=self.tau_actions, n_iters=self.sinkhorn_iters)
            P_actions.append(P_i)

        canon = ordinated_payoffs
        for i, P_i in enumerate(P_actions):
            canon = self._mode_matmul(canon, P_i, axis=1 + i)

        s_players = self._player_scores(canon)
        P_players = self.soft_perm_from_scores(s_players, tau=self.tau_players, n_iters=self.sinkhorn_iters)
        canon = self._mode_matmul(canon, P_players, axis=0)

        return canon, P_players, tuple(P_actions)

Hard Canonicalization

We also want a “hard” path to verify everything is working properly. We can map the “soft” permutations back to “hard” permutations and then use those to recover the discrete cases.

Project Soft Permutations to Hard

The _project_soft_to_perm method converts a soft permutation matrix to a hard permutation (using the Hungarian algorithm). We add tiny tie-breaking noise to ensure deterministic results even when the soft matrix has ambiguous assignments.

    @staticmethod
    def _project_soft_to_perm(P_soft: torch.Tensor) -> torch.Tensor:
        n = P_soft.shape[0]
        idx = torch.arange(n, device=P_soft.device, dtype=P_soft.dtype)
        eps = 1e-11 * (idx[:, None] + 0.73 * idx[None, :])

        cost = (-P_soft + eps).detach().cpu().numpy()
        r, c = hungarian(cost)
        Pi = torch.zeros_like(P_soft)
        Pi[r, c] = 1.0
        return Pi

Lexicographic Ordering For Symmetric Games

The _axis_lexperm method performs lexicographic sorting along a specified axis, which is crucial for handling symmetric games like Matching Pennies. It treats each slice along the axis as a multi-digit number in base (max_rank + 1) and sorts these “numbers” to get a canonical ordering. The _permute_along_axis helper applies the resulting permutation to reorder the tensor. This deterministic tie-breaking ensures that even perfectly symmetric games get a unique canonical form.

    def _axis_lexperm(self, ranks: torch.Tensor, axis: int) -> torch.Tensor:

        perm = list(range(ranks.ndim))
        perm[axis], perm[0] = perm[0], perm[axis]
        X = ranks.permute(perm) 

        n = X.shape[0]
        S = X.reshape(n, -1)

        maxv = int(S.max().item()) if S.numel() > 0 else 0
        base = maxv + 1

        K = torch.zeros(n, dtype=torch.float64, device=S.device)
        pow_ = 1.0
        for j in range(S.shape[1]-1, -1, -1):
            K += (S[:, j].to(torch.float64)) * pow_
            pow_ *= base

        order = torch.argsort(K, stable=True)
        return order

    @staticmethod
    def _permute_along_axis(t: torch.Tensor, order: torch.Tensor, axis: int) -> torch.Tensor:
        perm = list(range(t.ndim))
        perm[axis], perm[0] = perm[0], perm[axis]
        t0 = t.permute(perm)
        t0 = t0.index_select(0, order.to(t0.device))
        inv = list(range(t.ndim))
        inv[0], inv[axis] = inv[axis], inv[0]
        return t0.permute(inv)

Integer Ordinals

The _integerize_ordinals method converts soft ordinal rankings to hard integer ranks (0, 1, 2, 3 for 2×2 games). It adds tiny deterministic noise based on the golden ratio to break ties, then uses argsort twice to get proper rankings. This ensures each player’s outcomes are mapped to distinct integers while preserving the ordering from the soft ranks.

    @staticmethod
    def _integerize_ordinals(ord_tensor: torch.Tensor) -> torch.Tensor:
        P = ord_tensor.shape[0]
        M = ord_tensor[0].numel()
        out = []
        for p in range(P):
            x = ord_tensor[p].flatten()
            idx = torch.arange(M, device=x.device, dtype=x.dtype)
            x_eps = x + 1e-9 * ((idx * 0.61803398875) % 1.0) # Golden ratio trick
            order = torch.argsort(x_eps, stable=True)      
            ranks = torch.empty_like(order)
            ranks[order] = torch.arange(M, device=x.device)
            out.append(ranks.view_as(ord_tensor[p]))
        return torch.stack(out, dim=0).to(torch.int32)

Putting it Together

The hard_canonical method performs the complete canonicalization with hard permutations. It follows the same flow as the soft version but uses the Hungarian algorithm via _project_soft_to_perm to convert each soft permutation to a hard one. After applying player and action permutations, it performs an additional lexicographic sorting step on the integer ordinals to handle symmetric games. This final step ensures a unique canonical form even when the initial permutations leave multiple valid orderings.

    def hard_canonical(self, payoffs: torch.Tensor):
        P = payoffs.shape[0]

        ordinal = self.ordinate(payoffs)

        Pi_actions = []
        hard = ordinal
        for i in range(P):
            s_actions = self._action_scores(ordinal[i], player_idx=i)
            P_i_soft = self.soft_perm_from_scores(s_actions, tau=self.tau_actions, n_iters=self.sinkhorn_iters)
            Pi_i = self._project_soft_to_perm(P_i_soft.detach())
            hard = self._mode_matmul(hard, Pi_i, axis=1 + i)
            Pi_actions.append(Pi_i)

        s_players = self._player_scores(hard)
        P_players_soft = self.soft_perm_from_scores(s_players, tau=self.tau_players, n_iters=self.sinkhorn_iters)
        Pi_players = self._project_soft_to_perm(P_players_soft.detach())
        hard = self._mode_matmul(hard, Pi_players, axis=0)

        ranks = self._integerize_ordinals(hard)

        order0 = self._axis_lexperm(ranks, axis=0)

        E0_h = torch.eye(P, device=hard.device, dtype=hard.dtype)[order0]
        hard  = self._mode_matmul(hard, E0_h, axis=0)

        ranks = self._permute_along_axis(ranks, order0, axis=0)

        for i in range(P):
            ord_i = self._axis_lexperm(ranks, axis=1 + i)

            # float path
            n_i  = hard.shape[1 + i]
            Ei_h = torch.eye(n_i, device=hard.device, dtype=hard.dtype)[ord_i]
            hard  = self._mode_matmul(hard, Ei_h, axis=1 + i)

            # int path
            ranks = self._permute_along_axis(ranks, ord_i, axis=1 + i)
        return hard, Pi_players, tuple(Pi_actions)

Hashing

The class_id method generates a unique identifier for each game’s strategic equivalence class. It runs the hard canonicalization, converts the result to integer ordinals, then computes a SHA-256 hash of the binary representation. This allows us to quickly identify when two games are strategically equivalent.

    def class_id(self, payoffs: torch.Tensor):
        hard_ord, _, _ = self.hard_canonical(payoffs)
        ranks = self._integerize_ordinals(hard_ord)
        b = ranks.detach().cpu().numpy().tobytes()
        digest = hashlib.sha256(b).hexdigest()
        return digest[:12], digest, ranks

Complexity Analysis

The canonicalization process has the following complexity for 2×2 games: - Ordinal ranking: \(O(n \log n)\) where n = 4 (number of outcomes per player) - Sinkhorn iterations: \(O(m × n^2)\) where \(m\) is the number of iterations - Hungarian algorithm for hard permutation: \(O(n^3)\)

For 2×2 games, this is effectively constant time. For larger games with \(n\) players and \(k\) strategies each: - Space: \(O(n × k^n)\) for the payoff tensor - Time: \(O(n × k^n × log(k^n))\) for ranking + \(O(n × m × k^2)\) for permutations

Edge Cases and Limitations

This implementation handles several tricky cases:

1. Symmetric games (e.g., Matching Pennies): The lexicographic ordering ensures deterministic canonicalization even when multiple permutations could be valid.

2. Ties in ordinal rankings: While we assume strict ordinal games, near-ties are handled via the tie-breaking parameters tiny_tie.

The main limitation is the restriction to strict ordinal games. Games with payoff ties would require a different approach or explicit tie-breaking rules.

Example

Let’s look at a simple example.

# Our original games from the introduction
game_a = torch.tensor([
    [[3.0, 0.0],[5.0, 1.0]],
    [[3.0, 5.0],[0.0, 1.0]],
])

game_b = torch.tensor([
    [[10.0, 25.0],[4.0, 16.0]],
    [[10.0, 4.0],[25.0, 16.0]],
])

canon = GameCanonicalizer(num_players=2)

# Ordinal conversion
ord_a = canon.ordinate(game_a)
# [[2, 0], [3, 1]] for P1, [[2, 3], [0, 1]] for P2

ord_b = canon.ordinate(game_b) 
# [[1, 3], [0, 2]] for P1, [[1, 0], [3, 2]] for P2

# Canonicalization
canon_a, _, _ = canon.hard_canonical(game_a)
canon_b, _, _ = canon.hard_canonical(game_b)

# Verify they're the same
id_a = canon.class_id(game_a)[0]
id_b = canon.class_id(game_b)[0]

print(f"Game A canonical: {canon_a}")
print(f"Game B canonical: {canon_b}")
print(f"Game A ID: {id_a}")
print(f"Game B ID: {id_b}")
print(f"Same game? {id_a == id_b}")  # True!

Tests

Let’s now look at some tests. We’ll start with some helper functions⁸.

Helper Functions

def affine(payoffs: torch.Tensor, a0=1.0, b0=0.0, a1=1.0, b1=0.0) -> torch.Tensor:
    P = payoffs.clone().float()
    P[0] = a0 * P[0] + b0
    P[1] = a1 * P[1] + b1
    return P

def permute_actions(payoffs: torch.Tensor, perm0=(0,1), perm1=(0,1)) -> torch.Tensor:
    P = payoffs.clone()
    P = P[:, perm0, :]   
    P = P[:, :, perm1]  
    return P

def swap_players(payoffs: torch.Tensor) -> torch.Tensor:
    P0 = payoffs[0].transpose(0,1)  
    P1 = payoffs[1].transpose(0,1)
    return torch.stack([P1, P0], dim=0)

def class_id(canon, U):
    short, full, _ = canon.class_id(U)
    return full 

The first three functions will let us create variants of games. The last function returns the full class_id for a given game.

Game Payoffs

Here’s a number of “base games” we can test:

def prisoners_dilemma():
    return torch.tensor([
        [[3.0, 0.0],[5.0, 1.0]],
        [[3.0, 5.0],[0.0, 1.0]],
    ])

def stag_hunt():
    return torch.tensor([
        [[4.0, 0.0],[3.0, 3.0]],
        [[4.0, 3.0],[0.0, 3.0]],
    ])

def battle_of_sexes():
    return torch.tensor([
        [[2.0, 0.0],[0.0, 1.0]],
        [[1.0, 0.0],[0.0, 2.0]],
    ])

def matching_pennies():
    P1 = torch.tensor([[1.0, -1.0],[-1.0, 1.0]])
    P2 = -P1
    return torch.stack([P1, P2], dim=0)

def hawk_dove():
    return torch.tensor([
        [[0.0, 3.0],[1.0, 2.0]],
        [[0.0, 1.0],[3.0, 2.0]],
    ])

Stability Under Transformation

We can combine our base payoffs with our transfomation functions to build variants:

def pd_variants():
    U = prisoners_dilemma()
    return [
        U,
        affine(U, a0=2.0, b0=5.0, a1=0.5, b1=-1.0),                         
        permute_actions(U, perm0=(1,0), perm1=(1,0)),                       
        swap_players(U),                                                    
        permute_actions(affine(U, a0=3.0, b0=7.0, a1=1.7, b1=2.0), (1,0), (0,1)),  
    ]

def sh_variants():
    U = stag_hunt()
    return [
        U,
        affine(U, a0=4.0, b0=10.0, a1=2.0, b1=-3.0),
        permute_actions(U, perm0=(1,0), perm1=(1,0)),
        swap_players(U),
        permute_actions(affine(U, a0=0.7, b0=0.0, a1=5.0, b1=1.0), (0,1), (1,0)),
    ]

def bos_variants():
    U = battle_of_sexes()
    return [
        U,
        permute_actions(U, perm0=(1,0), perm1=(1,0)),   
        swap_players(U),                                  
        affine(U, a0=2.0, b0=1.0, a1=3.0, b1=-2.0),       
        permute_actions(affine(U, 1.0, 0.0, 4.0, 10.0), (1,0), (0,1)),
    ]

def mp_variants():
    U = matching_pennies()
    return [
        U,
        permute_actions(U, perm0=(1,0), perm1=(1,0)),     
        swap_players(U),                                   
        affine(U, a0=5.0, b0=3.0, a1=2.0, b1=-7.0),       
        permute_actions(affine(U, 2.0, 9.0, 1.0, -4.0), (1,0), (0,1)),
    ]

def hd_variants():
    U = hawk_dove()
    return [
        U,
        permute_actions(U, perm0=(1,0), perm1=(1,0)),
        swap_players(U),
        affine(U, a0=2.0, b0=0.0, a1=3.0, b1=1.0),
        permute_actions(affine(U, 0.5, 2.0, 1.5, -3.0), (0,1), (1,0)),
    ]

Then we can test this as so:

def test_family_equivalence(canonicalizer):
    families = [
        ("PrisonersDilemma", pd_variants()),
        ("StagHunt",         sh_variants()),
        ("BattleOfSexes",    bos_variants()),
        ("MatchingPennies",  mp_variants()),
        ("HawkDove",         hd_variants()),
    ]

    for name, variants in families:
        ids = [class_id(canonicalizer, U) for U in variants]
        assert len(set(ids)) == 1, f"{name}: expected all variants equivalent, got IDs: {ids}"
        print(f"[OK] {name}. ID {ids[0]} (x{len(variants)})")

Negative Controls

def test_negative_controls(canonicalizer):
    reps = [
        prisoners_dilemma(),
        stag_hunt(),
        battle_of_sexes(),
        matching_pennies(),
        hawk_dove(),
    ]
    ids = [class_id(canonicalizer, U) for U in reps]
    assert len(set(ids)) == len(ids), f"Negative control failed: collisions among base games: {ids}"
    print("[OK] Negative controls. Distinct IDs: ", ids)

Stability Under Small Noise

def test_stability_small_noise(canonicalizer):
    U = stag_hunt()
    base = class_id(canonicalizer, U)
    eps = 1e-9
    U_noisy = U + eps * torch.randn_like(U)
    pert = class_id(canonicalizer, U_noisy)
    assert base == pert, "Tiny noise changed ID; consider epsilon tie-handling."
    print("[OK] Stability to tiny noise.")

Conclusion

We have successfully constructed a differentiable way to produce a unique identifier for each strict ordinal 2x2 game. In the next post in this series, we will expand on this capability (or incorporate it into another pipeline for some practical use case).

Footnotes

1. Or vice-versa, to retrieve the game behavior based on some identifier.

2. i.e. “When does Stag Hunt turn into Chicken?” Hopefully more on this in a future post.

3. For an \(n\)-player, \(k\)-strategy game, we would need an \(n\times k \times ... \times k\) tensor (\(n\) copies of \(k\)).

4. I will hopefully also further investigate the algebraic structure of games, and this periodic table, in a future post.

5. Other forms of strategic equivalence might revolve around dominance relationships or best-response correspondences.

6. See Myerson (1991), Game Theory: Analysis of Conflict, Chapter 3.

7. There are alternative methods. From Claude: NeuralSort (Grover et al., 2019), SoftSort (Prillo & Eisenschlos, 2020), Fast Differentiable Sorting (Blondel et al., 2020), Optimal Transport Sort (Cuturi et al., 2019), Blackbox Differentiable Ranking (Vlastelica et al., 2020; Rolínek et al., 2020), Relaxed Bubble Sort (Petersen et al., 2021). We could also use non-differentiable methods, like REINFORCE. Sinkhorn should be sufficient for these purposes: it’s well-known, controllable, and stable, even for near-ties (common in symmetric games). If we need a faster algorithm later we can swap Sinkhorn for something else.

8. Disclosure: ChatGPT and Claude helped write the tests.