Differential Games and Stag Hunt

Introduction

In the last two posts in this series we looked at games as static functions with discrete strategies. That is, each player picked a strategy \(s_i \in S_i\) and at the end of the game the payoffs for each player were assessed as \(u_i(s_1,...,s_n)\).

Some games progress not across discrete strategies, but rather across continuous strategies (or strategies continuous in space and time). These games are called “differential games”. In this post, I attempt to construct a continuous version of stag hunt, and a general framework for simulating differential games. The intent here is to enable in-depth exploration of multi-agent control in subsequent posts.

Differential Games

We can think of differential games as an extension of both control theory and game theory, which both in turn extend discrete controls. In a typical Markov decision process/discrete control problem, we use techniques like dynamic programming to help determine the optimal policy for a single agent over a discrete state/action space. Game theory extends discrete control to \(n\)-agents, while classical control theory extends discrete control to a continuous state/action space. Differential games has \(n\)-agents operating in a continuous state/action space.

More formally, in a differential game, each player controls a control input \(u_i(t)\), and the state of the world \(x(t)\) evolves according to a differential equation

\[ \dot{x}(t) = f(x(t), u_1(t),..., u_n(t)) \]

Each agent receives some payoff \(J_i\) that is a combination of a trajectory factor (an instantaneous loss function \(L_i\) integrated over time) and a terminal factor \(g_i\):

\[ J_i = \int_0^T L_i(x(t), u_1(t), ..., u_n(t)) dt + g_i(x(T)) \]

We can also think of differential games as continuous-time differentiable programs. Each player’s policy \(\pi_i(o_i(t))\) is a differentiable function of its observation, and the dynamics \(f(x,u)\) act as a differentiable layer integrating the world forward alongside a natural loss function \(L\). This perspective allows us to use modern machine learning tools to analyze equilibria in continuous environments.

Code Architecture

Let’s lay out the requirements to define differential games in Python. We will build up the software in layers. The main concern here is separating game definition from game execution. We will use a similar model to the one laid out in previous posts on classical game theory. First we will implement a “physics” layer, which will manage state. Then we will implement a “decision” layer, agents make choices within those physics¹. Finally, we will have an Arena object that runs simulations and analyses on the outcomes.

Why do this? There are a few reasons:

1. State as immutable snapshots: We will bundle physical state, time, and payoffs as an immutable object. This enables branching, what-if analysis, and caching.
2. Pure simulation functions: Our tick and simulate functions are pure functions. This makes the simulator composable: you can pause mid-game, fork multiple futures, or replay with different policies. This is important for model-predictive control and counterfactual reasoning.
3. Differentiability everywhere: Since functions are pure, every component can support automatic differentiation. This will lets us backpropagate through entire trajectories to learn optimal policies via gradient descent.

We’ll look at the code in the next section².

Physics Layer

State Spaces

The first layer is the state space layer. We will keep the actual state specifications abstract so that they can apply to a multitude of different games. Each agent will have its own state, and the game may have a shared state as well.

The StateSpace object takes a list of agents and a shared state object and produce a single object maintaining the entire state, plus getters and setters for altering and retrieving different aspects of the state.

@dataclass
class StateSpec:
    names: List[str]  # e.g., ['x', 'y', 'vx', 'vy']
    
    def dim(self) -> int:
        return len(self.names)

class StateSpace:
    
    def __init__(self, 
                 agents: List['Agent'],
                 shared_spec: Optional[StateSpec] = None):

        self.agents = agents
        self.agent_names = [a.name for a in agents]
        self.agent_dims = {a.name: a.state_spec.dim() for a in agents}
        self.shared_dim = shared_spec.dim() if shared_spec else 0
        
        self.slices, self.dim = self._build_state_indexing()
    
    def _build_state_indexing(self) -> Tuple[Dict[str, slice], int]:
        slices = {}
        offset = 0
        
        for agent_name in self.agent_names:
            dim = self.agent_dims[agent_name]
            slices[agent_name] = slice(offset, offset + dim)
            offset += dim
        
        if self.shared_dim > 0:
            slices['shared'] = slice(offset, offset + self.shared_dim)
            offset += self.shared_dim
        
        return slices, offset
    
    def zero(self) -> torch.Tensor:
        return torch.zeros(self.dim)
    
    def get_state(self, state: torch.Tensor, agent: str) -> torch.Tensor:
        return state[self.slices[agent]]
    
    def get_shared(self, state: torch.Tensor) -> torch.Tensor:
        if self.shared_dim > 0:
            return state[self.slices['shared']]
        return torch.tensor([])
    
    def set_state(self, state: torch.Tensor, agent: str, value: torch.Tensor):
        state[self.slices[agent]] = value

Lastly, we need the actual GameState object:

@dataclass
class GameState:
    
    physical_state: torch.Tensor 
    time: float
    cumulative_payoffs: Dict[str, float]
    metadata: Dict[str, Any] = field(default_factory=dict)
    
    def clone(self) -> 'GameState':
        """Deep copy for branching"""
        return GameState(
            physical_state=self.physical_state.clone(),
            time=self.time,
            cumulative_payoffs=self.cumulative_payoffs.copy(),
            metadata=self.metadata.copy()
        )
    
    def with_state(self, new_physical_state: torch.Tensor) -> 'GameState':
        """Return new GameState with updated physical state"""
        return GameState(
            physical_state=new_physical_state,
            time=self.time,
            cumulative_payoffs=self.cumulative_payoffs,
            metadata=self.metadata
        )
    
    def with_time(self, new_time: float) -> 'GameState':
        """Return new GameState with updated time"""
        return GameState(
            physical_state=self.physical_state,
            time=new_time,
            cumulative_payoffs=self.cumulative_payoffs,
            metadata=self.metadata
        )
    
    def add_payoffs(self, step_payoffs: Dict[str, float]) -> 'GameState':
        """Return new GameState with updated payoffs"""
        new_payoffs = self.cumulative_payoffs.copy()
        for agent, reward in step_payoffs.items():
            new_payoffs[agent] = new_payoffs.get(agent, 0.0) + reward
        
        return GameState(
            physical_state=self.physical_state,
            time=self.time,
            cumulative_payoffs=new_payoffs,
            metadata=self.metadata
        )

This is the immutable snapshot of the state at any given point in time.

Observations

Given the state, each agent will need to observe part of it (depending on the game). We define an ObservationModel to handle this.

class ObservationModel(ABC):
    
    @abstractmethod
    def observe(self, state: torch.Tensor, agent: str, cumulative_payoff: Optional[float] = None) -> torch.Tensor:
        pass
    
    @abstractmethod
    def obs_dim(self, agent: str) -> int:
        pass

Dynamics

Next we have dynamics. The dynamics determine how the world actually evolves. Here’s the abstract interface.

class Dynamics(ABC):
    
    @abstractmethod
    def derivative(self, 
                   state: torch.Tensor,
                   controls: Dict[str, torch.Tensor]) -> torch.Tensor:
        pass

We hand the dynamics a state and controls and it outputs the change in state³.

Constraints

Real systems have constraints: agents can’t leave the arena, they can’t pass through walls, they shouldn’t collide with each other. We handle constraints in two ways. The first is soft violations (violated()), a differentiable penalty that grows outside the feasible region, used during learning or optimization. The second is hard projection (project()), which pushes the state back onto the constraint surface and is used to enforce physics.

Here’s the abstract interface:

class Constraint(ABC):
    
    @abstractmethod
    def violated(self, state: torch.Tensor) -> torch.Tensor:
        """
        Returns violation amount (0 = satisfied, >0 = violated).
        Must be differentiable
        """
        pass
    
    @abstractmethod
    def project(self, state: torch.Tensor) -> torch.Tensor:
        """Project state onto feasible set"""
        pass

Here’s some examples:

class BoundaryConstraint(Constraint):
    """Box boundaries [x_min, x_max] × [y_min, y_max]"""
    
    def __init__(self, state_space: StateSpace, bounds: Dict[str, Tuple[float, float]]):
        """bounds = {'x': (min, max), 'y': (min, max)}"""
        self.state_space = state_space
        self.bounds = bounds
    
    def violated(self, state):
        # Soft violation for differentiability
        violation = 0.0
        for agent in self.state_space.agent_names:
            pos = self.state_space.get_state(state, agent)[:2]
            # Penalty grows quadratically outside bounds
            violation += torch.relu(self.bounds['x'][0] - pos[0])**2
            violation += torch.relu(pos[0] - self.bounds['x'][1])**2
            violation += torch.relu(self.bounds['y'][0] - pos[1])**2
            violation += torch.relu(pos[1] - self.bounds['y'][1])**2
        return violation
    
    def project(self, state):
        """Hard projection (like game engine collision resolution)"""
        new_state = state.clone()
        for agent in self.state_space.agent_names:
            pos = self.state_space.get_state(state, agent)[:2]
            # Clamp position
            pos_clamped = torch.stack([
                torch.clamp(pos[0], self.bounds['x'][0], self.bounds['x'][1]),
                torch.clamp(pos[1], self.bounds['y'][0], self.bounds['y'][1])
            ])
            # Reflect velocity if hit boundary
            vel = self.state_space.get_state(state, agent)[2:4]
            vel_new = vel.clone()
            if pos[0] <= self.bounds['x'][0] or pos[0] >= self.bounds['x'][1]:
                vel_new[0] *= -0.8  # Bounce with damping
            if pos[1] <= self.bounds['y'][0] or pos[1] >= self.bounds['y'][1]:
                vel_new[1] *= -0.8
            
            self.state_space.set_state(new_state, agent, 
                                torch.cat([pos_clamped, vel_new]))
        return new_state

class CollisionConstraint(Constraint):
    """Agent-agent collision avoidance"""
    
    def __init__(self, state_space, radius=0.3):
        self.state_space = state_space
        self.radius = radius
    
    def violated(self, state):
        violation = 0.0
        for i, a1 in enumerate(self.state_space.agent_names):
            for a2 in self.state_space.agent_names[i+1:]:
                dist = torch.norm(
                    self.state_space.get_state(state, a1)[:2] - 
                    self.state_space.get_state(state, a2)[:2]
                )
                # Soft barrier
                violation += torch.relu(self.radius - dist)**2
        return violation
    
    def project(self, state):
        # Separate overlapping agents (like game engine)
        new_state = state.clone()
        for i, a1 in enumerate(self.state_space.agent_names):
            for a2 in self.state_space.agent_names[i+1:]:
                p1 = self.state_space.get_state(state, a1)[:2]
                p2 = self.state_space.get_state(state, a2)[:2]
                dist = torch.norm(p1 - p2)
                if dist < self.radius:
                    # Push apart
                    direction = (p1 - p2) / (dist + 1e-6)
                    overlap = self.radius - dist
                    # Each moves half the overlap
                    # (would need to update both states)
        return new_state

Payoffs

In differential games, payoffs typically have two components. The first is a running cost, associated with the trajectory, and the second is the terminal reward, assessed at the final stage.

class PayoffModel(ABC):
    
    @abstractmethod
    def agents(self) -> List[str]:
        """Return list of agent names"""
        pass
    
    def step(self, 
             state: torch.Tensor, 
             controls: Dict[str, torch.Tensor], 
             dt: float) -> Dict[str, float]:
        """Incremental payoff for this timestep (override for running costs)"""
        return {a: 0.0 for a in self.agents()}
    
    def terminal(self, state: torch.Tensor) -> Dict[str, float]:
        """Terminal payoff (override for end-of-game rewards)"""
        return {a: 0.0 for a in self.agents()}
    
    def total(self, 
              trajectory: List[Tuple[torch.Tensor, Dict[str, torch.Tensor]]], 
              final_state: torch.Tensor,
              dt: float) -> Dict[str, float]:
        """
        Total payoff over trajectory.
        Default: sum step payoffs + terminal.
        Override for discounting, non-additive payoffs, etc.
        """
        total = {a: 0.0 for a in self.agents()}
        
        for state, controls in trajectory:
            step_payoff = self.step(state, controls, dt)
            for a in self.agents():
                total[a] += step_payoff[a]
        
        terminal_payoff = self.terminal(final_state)
        for a in self.agents():
            total[a] += terminal_payoff[a]
        
        return total

Integration

To integrate the dynamics forward in time, we need a numerical integrator. The integrator takes the derivative from Dynamics and produces the next state. We support multiple schemes with different accuracy/speed tradeoffs:

class Integrator(ABC):
    
    def step(self,
             dynamics: Dynamics,
             state: torch.Tensor,
             controls: Dict[str, torch.Tensor],
             dt: float,
             constraints: Optional[List[Constraint]] = None) -> torch.Tensor:
        """
        Integrate one timestep and project onto constraints.
        
        Args:
            dynamics: dynamics model
            state: current state
            controls: control inputs
            dt: timestep
            constraints: optional list of constraints to enforce
            
        Returns:
            new_state (after constraint projection if provided)
        """
        # Integration
        new_state = self._integrate(dynamics, state, controls, dt)
        
        # Constraint projection (automatic if constraints provided)
        if constraints:
            for constraint in constraints:
                new_state = constraint.project(new_state)
        
        return new_state
    
    @abstractmethod
    def _integrate(self,
                   dynamics: Dynamics,
                   state: torch.Tensor,
                   controls: Dict[str, torch.Tensor],
                   dt: float) -> torch.Tensor:
        """Actual integration scheme (implemented by subclasses)"""
        pass

class EulerIntegrator(Integrator):
    
    def _integrate(self, dynamics, state, controls, dt):
        dstate = dynamics.derivative(state, controls)
        return state + dstate * dt

class RK4Integrator(Integrator):
    
    def _integrate(self, dynamics, state, controls, dt):
        k1 = dynamics.derivative(state, controls)
        k2 = dynamics.derivative(state + 0.5 * dt * k1, controls)
        k3 = dynamics.derivative(state + 0.5 * dt * k2, controls)
        k4 = dynamics.derivative(state + dt * k3, controls)
        return state + (dt / 6.0) * (k1 + 2*k2 + 2*k3 + k4)

Decision Layer

The next layer of code determines how agents actually behave.

Policy

A policy maps observations to control actions: \(u = \pi(o)\).

class Policy(ABC):
    """Observation to control"""
    
    @abstractmethod
    def __call__(self, obs: torch.Tensor) -> torch.Tensor:
        """Must be differentiable for learning"""
        pass
    
    @abstractmethod
    def control_dim(self) -> int:
        pass

There are two kinds of policies: learnable ( use neural networks with parameters we can optimize via gradient descent) and hand-crafted (regular Python functions, useful for baselines, testing, etc).

class NeuralPolicy(Policy, nn.Module):
    """Learnable policy"""
    
    def __init__(self, obs_dim: int, control_dim: int, hidden_dim: int = 64):
        Policy.__init__(self)
        nn.Module.__init__(self)
        self._control_dim = control_dim
        
        self.net = nn.Sequential(
            nn.Linear(obs_dim, hidden_dim),
            nn.Tanh(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.Tanh(),
            nn.Linear(hidden_dim, control_dim),
            nn.Tanh(),  # Bounded output
        )
        
        # Small init for stability
        for m in self.net.modules():
            if isinstance(m, nn.Linear):
                nn.init.orthogonal_(m.weight, gain=0.1)
                nn.init.zeros_(m.bias)
    
    def __call__(self, obs: torch.Tensor) -> torch.Tensor:
        return nn.Module.__call__(self, obs)
    
    def forward(self, obs: torch.Tensor) -> torch.Tensor:
        return self.net(obs)
    
    def control_dim(self) -> int:
        return self._control_dim

class FunctionPolicy(Policy):
    """Hand-coded policy (can be differentiable or not)"""
    
    def __init__(self, 
                 fn: Callable[[torch.Tensor], torch.Tensor],
                 control_dim: int,
                 differentiable: bool = False):
        self.fn = fn
        self._control_dim = control_dim
        self.differentiable = differentiable
    
    def __call__(self, obs: torch.Tensor) -> torch.Tensor:
        if self.differentiable:
            return self.fn(obs)
        else:
            with torch.no_grad():
                return self.fn(obs)
    
    def control_dim(self) -> int:
        return self._control_dim

Agents

An Agent bundles together a state specification (what variables it tracks) and a set of named strategies (the policies it can choose from). This bridges the gap between continuous control (policies) and discrete game theory (strategy names like “Cooperate” or “Defect”).

class Agent:
    """Agent with state specification and named strategies"""
    
    def __init__(self,
                 name: str,
                 state_spec: StateSpec,
                 strategy_set: Dict[str, Policy]):
        """
        Args:
            name: agent identifier
            state_spec: symbolic state specification
            strategy_set: dict of strategy_name -> Policy
        """
        self.name = name
        self.state_spec = state_spec
        self.strategy_set = strategy_set
        self.strategy_names = list(strategy_set.keys())
    
    def get_policy(self, strategy_name: str) -> Policy:
        return self.strategy_set[strategy_name]

Game Definitions

Here’s the actual definition of our differential game. We need a StateSpace, a list of agents (wiht observation models, dynamics, and payoff models), and an initial sampler.

class DifferentialGame:
    def __init__(self,
                 state_space: StateSpace,
                 agents: List[Agent],
                 obs_model: ObservationModel,
                 dynamics: Dynamics,
                 payoff_model: PayoffModel,
                 initial_sampler: Callable[[], torch.Tensor],
                 name: str = "Differential Game"):
        self.state_space = state_space
        self.agents = {a.name: a for a in agents}
        self.agent_names = [a.name for a in agents]
        self.obs_model = obs_model
        self.dynamics = dynamics
        self.payoff_model = payoff_model
        self.initial_sampler = initial_sampler
        self.name = name
    
    def get_strategy_sets(self) -> Dict[str, List[str]]:
        """Get available strategies per agent"""
        return {name: agent.strategy_names for name, agent in self.agents.items()}
    
    def __repr__(self):
        return f'<DifferentialGame "{self.name}" agents={self.agent_names}>'

Game Execution Layer

Arena

The Arena object executes games. While DifferentialGame defines the rules, Arena actually simulates trajectories. This separation means you can define a game once, then run it with different: - Strategy profiles (cooperate vs defect) - Initial conditions (different starting positions) - Integration methods (Euler vs RK4) - Time horizons (short sprints vs long chases)

The core method is play(), which takes a strategy profile (mapping each agent to a strategy name) and returns the full trajectory plus final payoffs.

class Arena:
    
    def __init__(self,
                 game: DifferentialGame,
                 integrator: Integrator = None,
                 dt: float = 0.02,
                 max_time: float = 10.0):
        self.game = game
        self.integrator = integrator or EulerIntegrator()
        self.dt = dt
        self.max_time = max_time

    def initial_state(self, 
                      physical_state: Optional[torch.Tensor] = None) -> GameState:
        if physical_state is None:
            physical_state = self.game.initial_sampler()
        
        return GameState(
            physical_state=physical_state,
            time=0.0,
            cumulative_payoffs={agent: 0.0 for agent in self.game.agent_names}
        )

    def tick(self, 
             state: GameState, 
             policies: Dict[str, Policy],
             constraints: Optional[List[Constraint]] = None) -> GameState:

        # Observe
        observations = {
            agent: self.game.obs_model.observe(
                state.physical_state, 
                agent,
                state.cumulative_payoffs.get(agent, 0.0)
            )
            for agent in self.game.agent_names
        }
        
        # Act
        controls = {
            agent: policies[agent](observations[agent])
            for agent in self.game.agent_names
        }
        
        # Compute step payoffs (before state changes)
        step_payoffs = self.game.payoff_model.step(
            state.physical_state, 
            controls, 
            self.dt
        )
        
        # Integrate physics
        new_physical = self.integrator.step(
            self.game.dynamics,
            state.physical_state,
            controls,
            self.dt,
            constraints
        )
        
        # Build new state
        new_state = (state
                     .with_state(new_physical)
                     .with_time(state.time + self.dt)
                     .add_payoffs(step_payoffs))
        
        return new_state
    
    def simulate(self,
                 policies: Dict[str, Policy],
                 initial: Optional[GameState] = None,
                 until: Optional[float] = None,
                 constraints: Optional[List[Constraint]] = None) -> List[GameState]:
       
        if initial is None:
            initial = self.initial_state()
        
        end_time = until if until is not None else self.max_time
        
        trajectory = [initial]
        state = initial
        
        while state.time < end_time:
            state = self.tick(state, policies, constraints)
            trajectory.append(state)
        
        return trajectory

    def play(self,
             strategy_profile: Dict[str, str],
             initial: Optional[GameState] = None,
             constraints: Optional[List[Constraint]] = None) -> Tuple[List[GameState], Dict[str, float]]:

        # Convert strategy names to policies
        policies = {
            agent: self.game.agents[agent].get_policy(strategy_profile[agent])
            for agent in self.game.agent_names
        }
        
        # Simulate
        trajectory = self.simulate(policies, initial, constraints=constraints)
        
        # Add terminal payoffs
        final_state = trajectory[-1]
        terminal_payoffs = self.game.payoff_model.terminal(final_state.physical_state)
        
        total_payoffs = final_state.cumulative_payoffs.copy()
        for agent, reward in terminal_payoffs.items():
            total_payoffs[agent] += reward
        
        return trajectory, total_payoffs
    
    def expected_payoffs(self,
                        strategy_profile: Dict[str, str],
                        n_samples: int = 100) -> Dict[str, float]:

        total_payoffs = {agent: 0.0 for agent in self.game.agent_names}
        
        for _ in range(n_samples):
            _, payoffs = self.play(strategy_profile, initial=None)  # Random init each time
            for agent in self.game.agent_names:
                total_payoffs[agent] += payoffs[agent]
        
        return {agent: total_payoffs[agent] / n_samples for agent in self.game.agent_names}

Analysis

Converting to Normal Form

One of the unique features of this framework is the ability to convert continuous differential games back into discrete normal form. This lets us use all our existing game theory tools, like finding Nash equilibria, computing evolutionary dynamics, and visualizing payoff matrices.

class StrategyProfileIterator:
    """
    Iterate over all strategy profiles.
    Essential for converting differential game to normal form.
    """
    
    def __init__(self, strategy_sets: Dict[str, List[str]]):
        """
        strategy_sets: dict of agent -> list of strategy names
        """
        self.strategy_sets = strategy_sets
        self.agents = list(strategy_sets.keys())
    
    def __iter__(self):
        """Yield all strategy profiles"""
        strategy_lists = [self.strategy_sets[agent] for agent in self.agents]
        for profile_tuple in itertools.product(*strategy_lists):
            yield dict(zip(self.agents, profile_tuple))
    
    def count(self) -> int:
        """Total number of profiles"""
        count = 1
        for strategies in self.strategy_sets.values():
            count *= len(strategies)
        return count


class NormalFormConverter:
    """Convert differential game to normal form """
    
    @staticmethod
    def to_payoff_matrix(arena: Arena,
                        players: List[str],
                        n_samples: int = 1) -> torch.Tensor:
        """
        Convert to normal form payoff tensor.
        
        Args:
            arena: Arena with differential game
            players: list of player names to include (typically subset of 2)
            n_samples: number of samples per profile (for averaging)
            
        Returns:
            payoff tensor with shape (n_players, *strategy_dims)
        """
        # Get strategy sets for selected players
        all_sets = arena.game.get_strategy_sets()
        strategy_sets = {p: all_sets[p] for p in players}
        
        # Other agents use first strategy by default
        fixed_strategies = {
            agent: all_sets[agent][0]
            for agent in arena.game.agent_names
            if agent not in players
        }
        
        # Build tensor shape
        dims = [len(strategy_sets[p]) for p in players]
        payoff_shape = [len(players)] + dims
        payoffs = torch.zeros(payoff_shape)
        
        # Iterate over all profiles
        iterator = StrategyProfileIterator(strategy_sets)
        
        for profile in iterator:
            # Combine with fixed strategies
            full_profile = {**fixed_strategies, **profile}
            
            # Get indices for this profile
            indices = tuple(strategy_sets[p].index(profile[p]) for p in players)
            
            # Compute expected payoff
            if n_samples == 1:
                _, payoff_dict = arena.play(full_profile, differentiable=False)
            else:
                payoff_dict = arena.expected_payoffs(full_profile, n_samples)
            
            # Store in tensor
            for i, player in enumerate(players):
                payoffs[(i,) + indices] = payoff_dict[player]
        
        return payoffs

Visualization

Here’s also a visualization tool, to help see what’s going on in the game.

def plot_trajectory(trajectory: List[GameState],
                   state_space: StateSpace,
                   title: str = ""):
    """Plot 2D trajectories (assumes first 2 dims are x, y)"""
    fig, ax = plt.subplots(figsize=(8, 8))
    
    colors = {name: f'C{i}' for i, name in enumerate(state_space.agent_names)}
    
    for agent_name in state_space.agent_names:
        positions = []
        for game_state in trajectory:  # game_state is GameState
            state = game_state.physical_state  # ← Extract tensor
            agent_state = state_space.get_state(state, agent_name)
            positions.append(agent_state[:2])

        positions = np.array(positions)
        ax.plot(positions[:, 0], positions[:, 1],
               color=colors[agent_name], label=agent_name, alpha=0.7, linewidth=2)
        ax.scatter(positions[0, 0], positions[0, 1],
                  color=colors[agent_name], s=150, marker='o', edgecolor='black', linewidth=2)
        ax.scatter(positions[-1, 0], positions[-1, 1],
                  color=colors[agent_name], s=150, marker='X', edgecolor='black', linewidth=2)
    
    ax.set_aspect('equal')
    ax.legend()
    ax.grid(alpha=0.3)
    ax.set_title(title)
    plt.tight_layout()
    return fig

def plot_payoff_heatmap(payoff_tensor: torch.Tensor,
                       players: List[str],
                       strategy_sets: Dict[str, List[str]]):
    """Visualize 2-player payoff matrix"""
    if len(players) != 2:
        raise ValueError("Can only plot 2-player games")
    
    p1, p2 = players
    p1_strats = strategy_sets[p1]
    p2_strats = strategy_sets[p2]
    
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
    
    # Player 1 payoffs
    matrix1 = payoff_tensor[0].numpy()
    im1 = ax1.imshow(matrix1, cmap='RdYlGn', aspect='auto')
    ax1.set_xticks(range(len(p2_strats)))
    ax1.set_yticks(range(len(p1_strats)))
    ax1.set_xticklabels(p2_strats)
    ax1.set_yticklabels(p1_strats)
    ax1.set_xlabel(f'{p2} strategy')
    ax1.set_ylabel(f'{p1} strategy')
    ax1.set_title(f'{p1} Payoffs')
    
    for i in range(len(p1_strats)):
        for j in range(len(p2_strats)):
            ax1.text(j, i, f'{matrix1[i, j]:.1f}',
                    ha='center', va='center', fontsize=12, weight='bold')
    
    plt.colorbar(im1, ax=ax1)
    
    # Player 2 payoffs
    matrix2 = payoff_tensor[1].numpy()
    im2 = ax2.imshow(matrix2, cmap='RdYlGn', aspect='auto')
    ax2.set_xticks(range(len(p2_strats)))
    ax2.set_yticks(range(len(p1_strats)))
    ax2.set_xticklabels(p2_strats)
    ax2.set_yticklabels(p1_strats)
    ax2.set_xlabel(f'{p2} strategy')
    ax2.set_ylabel(f'{p1} strategy')
    ax2.set_title(f'{p2} Payoffs')
    
    for i in range(len(p1_strats)):
        for j in range(len(p2_strats)):
            ax2.text(j, i, f'{matrix2[i, j]:.1f}',
                    ha='center', va='center', fontsize=12, weight='bold')
    
    plt.colorbar(im2, ax=ax2)
    plt.tight_layout()
    return fig

Example: Stag Hunt

Now we’ll use this framework to build a pursuit-evasion game with stag hunt payoffs.

The setup is:

• There are 2 cooperative hunters (c1, c2)
• There is 1 stag (worth 4 points, requires both hunters to catch)
• There are 2 hares (worth 3 points each, can be caught by one hunter)
• The stag is faster than the hares but slower than hunters
• The hunters pursue using simple “move toward target” policies
• Prey flee using “move away from threats” policies

What differs from standard game theoretic stag hunt is that this plays out as a pursuit-evastion game in continuous space.

Definition

We define each agent as a point mass in 2D. The remaining code defines each element (including state positions) for each Agent.

POINT_MASS_2D = StateSpec(['x', 'y', 'vx', 'vy'])
POINT_MASS_3D = StateSpec(['x', 'y', 'z', 'vx', 'vy', 'vz'])

def build_stag_hunt():
    """Build stag hunt differential game"""
    
    # Build agents with strategies
    def make_pursuit(state_space, agent_name: str, targets: List[str], speed: float):
        def fn(obs):
            # obs is full state - extract this agent's position
            own_pos = state_space.get_state(obs, agent_name)[:2]
            target_pos = torch.stack([state_space.get_state(obs, t)[:2] for t in targets]).mean(dim=0)
            direction = target_pos - own_pos
            dist = torch.norm(direction) + 1e-6
            return (direction / dist) * speed
        return FunctionPolicy(fn, 2, differentiable=True)
    
    def make_flee(state_space, agent_name: str, threats: List[str], speed: float):
        def fn(obs):
            # obs is full state - extract this agent's position
            own_pos = state_space.get_state(obs, agent_name)[:2]
            threat_pos = torch.stack([state_space.get_state(obs, t)[:2] for t in threats]).mean(dim=0)
            direction = own_pos - threat_pos
            dist = torch.norm(direction) + 1e-6
            return (direction / dist) * speed
        return FunctionPolicy(fn, 2, differentiable=True)
    
    # Create agents with state specifications
    agents = [
        Agent('c1', POINT_MASS_2D, {}),  # Strategies added below
        Agent('c2', POINT_MASS_2D, {}),
        Agent('stag', POINT_MASS_2D, {}),
        Agent('hare1', POINT_MASS_2D, {}),
        Agent('hare2', POINT_MASS_2D, {}),
    ]
    
    # Build state space from agents
    state_space = StateSpace(agents, shared_spec=None)
    
    # Now add strategies (need state_space for closures)
    agents[0].strategy_set = {
        'ChaseStag': make_pursuit(state_space, 'c1', ['stag'], 1.5),
        'ChaseHare': make_pursuit(state_space, 'c1', ['hare1'], 1.5),
    }
    agents[0].strategy_names = list(agents[0].strategy_set.keys())
    
    agents[1].strategy_set = {
        'ChaseStag': make_pursuit(state_space, 'c2', ['stag'], 1.5),
        'ChaseHare': make_pursuit(state_space, 'c2', ['hare2'], 1.5),
    }
    agents[1].strategy_names = list(agents[1].strategy_set.keys())
    
    agents[2].strategy_set = {'Flee': make_flee(state_space, 'stag', ['c1', 'c2'], 1.1)}
    agents[2].strategy_names = list(agents[2].strategy_set.keys())
    
    agents[3].strategy_set = {'Flee': make_flee(state_space, 'hare1', ['c1', 'c2'], 0.6)}
    agents[3].strategy_names = list(agents[3].strategy_set.keys())
    
    agents[4].strategy_set = {'Flee': make_flee(state_space, 'hare2', ['c1', 'c2'], 0.6)}
    agents[4].strategy_names = list(agents[4].strategy_set.keys())
    
    # Observation: full state
    class FullObs(ObservationModel):
        def observe(self, state, agent):
            return state
        def obs_dim(self, agent):
            return state_space.dim
    
    obs_model = FullObs()
    
    # Dynamics: kinematic (differentiable!)
    all_agents = ['c1', 'c2', 'stag', 'hare1', 'hare2']
    
    class StagHuntPayoff(PayoffModel):
        def __init__(self, state_space, agent_names):
            self.state_space = state_space
            self._agents = agent_names
    
        def agents(self):
            return self._agents
    
        def terminal(self, state):    
            positions = {a: state_space.get_state(state, a)[:2] for a in all_agents}
        
            payoffs = {a: 0.0 for a in all_agents}
            radius = 0.5
            captured = {'c1': False, 'c2': False}
        
            # Stag (needs both)
            d1 = torch.norm(positions['c1'] - positions['stag']).item()
            d2 = torch.norm(positions['c2'] - positions['stag']).item()
        
            if d1 < radius and d2 < radius:
                payoffs['c1'] += 4.0
                payoffs['c2'] += 4.0
                captured['c1'] = True
                captured['c2'] = True
        
            # Hares (first come first served)
            if not captured['c1']:
                for hare in ['hare1', 'hare2']:
                    d = torch.norm(positions['c1'] - positions[hare]).item()
                    if d < radius:
                        payoffs['c1'] += 3.0
                        captured['c1'] = True
                        break
        
            if not captured['c2']:
                for hare in ['hare1', 'hare2']:
                    d = torch.norm(positions['c2'] - positions[hare]).item()
                    if d < radius:
                        payoffs['c2'] += 3.0
                        captured['c2'] = True
                        break
        
            return payoffs

    class KinematicDynamics(Dynamics):
        def __init__(self, max_speeds: Dict[str, float]):
            self.max_speeds = max_speeds
        
        def derivative(self, state, controls):
            dstate = []
            for agent in all_agents:
                agent_state = state_space.get_state(state, agent)
                control = controls[agent]
                
                # Soft clamping for differentiability
                vel_des = control
                speed = torch.norm(vel_des) + 1e-6
                max_speed = self.max_speeds[agent]
                
                # Soft clamp: vel = direction * min(speed, max_speed)
                scale_factor = max_speed * torch.tanh(speed / max_speed) / speed
                vel = vel_des * scale_factor
                
                dpos = vel
                dvel = torch.zeros(2)
                dstate.append(torch.cat([dpos, dvel]))
            
            return torch.cat(dstate)
    
    dynamics = KinematicDynamics({
        'c1': 1.5, 'c2': 1.5,
        'stag': 1.1, 'hare1': 0.6, 'hare2': 0.6
    })
    
    # Initial state
    def initial():
        return torch.cat([
            torch.tensor([-2.0, -2.0, 0.0, 0.0]),  # c1
            torch.tensor([2.0, -2.0, 0.0, 0.0]),   # c2
            torch.tensor([0.0, 2.0, 0.0, 0.0]),    # stag
            torch.tensor([-1.5, 0.0, 0.0, 0.0]),   # hare1
            torch.tensor([1.5, 0.0, 0.0, 0.0]),    # hare2
        ])
    
    payoff_model = StagHuntPayoff(state_space, all_agents)
    game = DifferentialGame(state_space, agents, obs_model, dynamics, payoff_model, initial, "Stag Hunt")
    
    return game, state_space

Results

Let’s see what the outputs look like:

if __name__ == "__main__": 
    game, state_space = build_stag_hunt()
    arena = Arena(game, dt=0.02, max_time=15.0)
    
    print(f"{game}")
    print(f"Strategy sets: {game.get_strategy_sets()}\n")
    
    # Test scenarios
    profiles = [
        ("Both Cooperate", {'c1': 'ChaseStag', 'c2': 'ChaseStag', 'stag': 'Flee', 'hare1': 'Flee', 'hare2': 'Flee'}),
        ("Both Defect", {'c1': 'ChaseHare', 'c2': 'ChaseHare', 'stag': 'Flee', 'hare1': 'Flee', 'hare2': 'Flee'}),
        ("Asymmetric", {'c1': 'ChaseStag', 'c2': 'ChaseHare', 'stag': 'Flee', 'hare1': 'Flee', 'hare2': 'Flee'}),
    ]
    
    for desc, profile in profiles:
        traj, payoffs = arena.play(profile)
        print(f"{desc}: c1={payoffs['c1']:.1f}, c2={payoffs['c2']:.1f}")
        plot_trajectory(traj, state_space, title=desc)
        plt.show()
    
    # Convert to normal form
    print("\n" + "="*60)
    print("NORMAL FORM EXTRACTION")
    print("="*60)
    
    payoff_tensor = NormalFormConverter.to_payoff_matrix(arena, ['c1', 'c2'], n_samples=1)
    print(f"\nPayoff tensor shape: {payoff_tensor.shape}")
    print(f"Payoff tensor:\n{payoff_tensor}")
    
    plot_payoff_heatmap(payoff_tensor, ['c1', 'c2'], game.get_strategy_sets())

We generate three plots. The first is the trajectories with both agents cooperating:

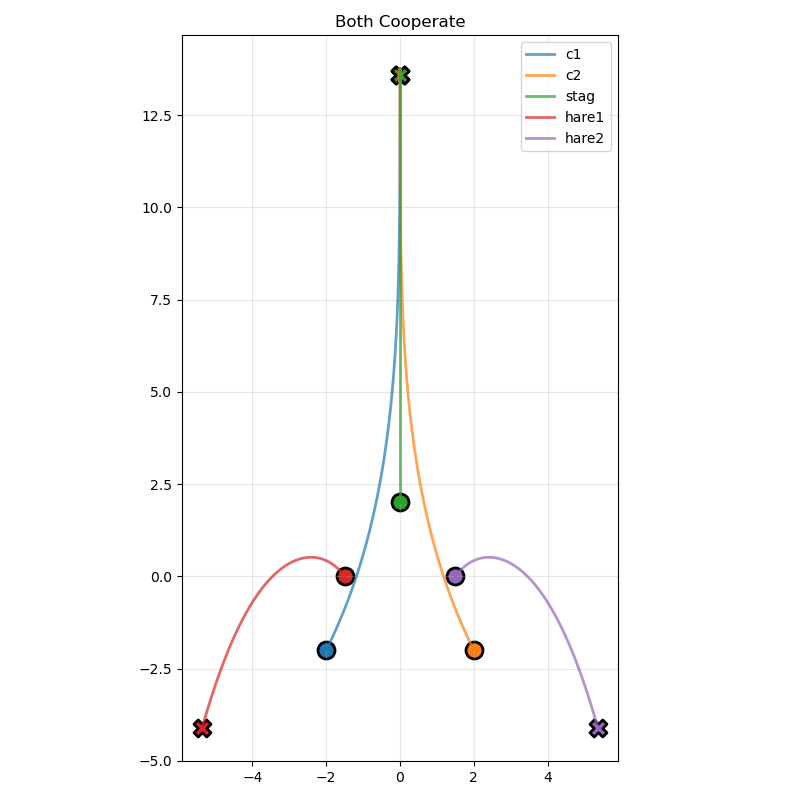
Second with two defections:

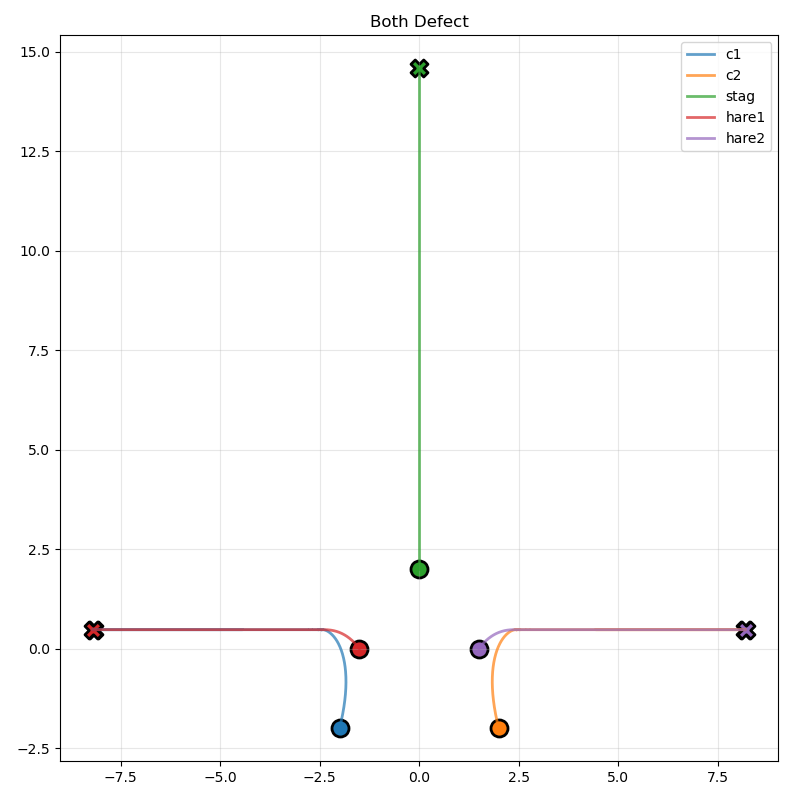
Third asymmetric:

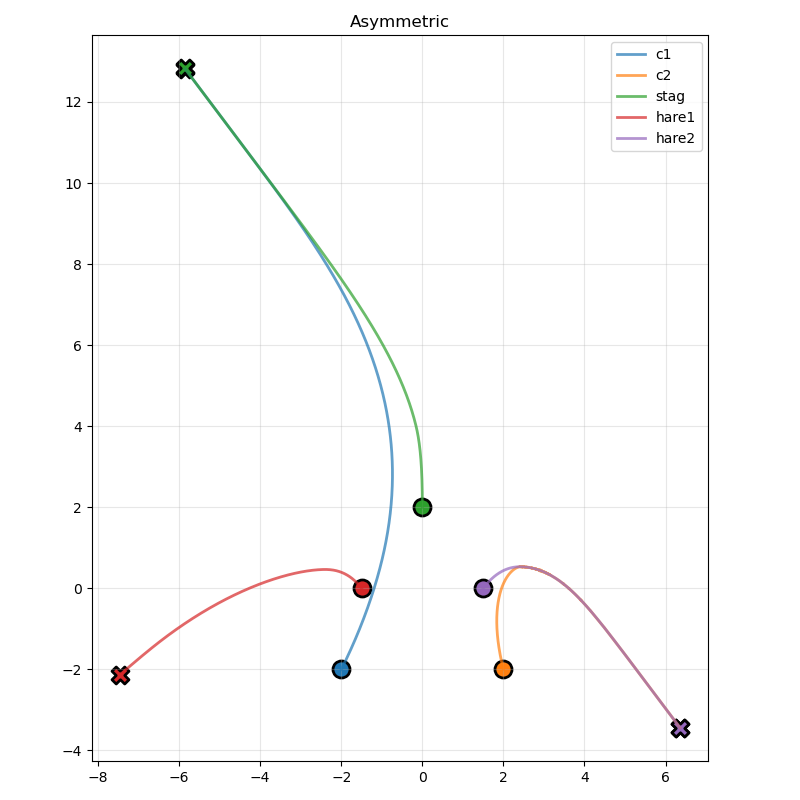
Conclusion and Next Steps

In this post, we implemented the beginnings of a differential games framework, then adapted it for pursuit-evasion games with two chasers and three heterogenous evaders. Specifically, the payoff structure of this game matches the well-known “stag hunt” game from game theory. In the next post, we will attempt to combine our differentiable game canonicalizer with this setup.

Footnotes

1. This is similar to how optimal control tools are architected, like Drake or Crocoddyl, or robotics simulatos (MuJoCo). I thought a bit about video game engines as well (Unity, Unreal Engine), but there the physics tend to be implicit and most of the abstractions are oriented around entities and components for building the actual content.

2. Disclosure: Claude helped with some functions, but I reviewed all code. I do not believe an AI could write this unassisted at time of writing.

3. For now, this the linearization of the change in state. In theory the dynamics could also support higher order derivations. Furthermore, right now this is manually computed. We might be able to use automatic differentiation to handle this as well. More on this in a future post.